|
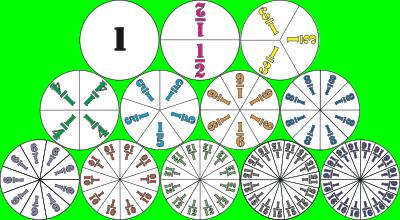
Fraction Circles
A requirement for teaching fractions effectively. Fraction rules are counterintuitive without them. Among the models for fractions, circles are the best because the unit is always evident: half a pie is half a pie no matter the size of the pie. In contrast, the unit for rods, squares, or rectangles is arbitrary. For instance, for the Cuisenaire rods, if the purple or 4-rod is the unit, the red or 2-rod is 1/2, but if later the orange or 10-rod is the unit, it is 1/5.
The most distinguishing feature of the fraction circles is that they depict 12 different fractions all the way out to 16ths: 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/9, 1/10, 1/12, 1/15, 1/16. (Sevenths, elevenths, and thirteenths were skipped because 7, 11, and 13 are prime numbers, thus severely limiting the number of problems that could be solved with them. Fourteenths were skipped because sevenths were skipped.) Having them go out that far allows students to solve lots of problems with them, and the more they solve, the more data (answers) they get from which to deduce the rules that connect the problems to the answers. Also, having 10ths, 15ths, and 16ths, in particular, make the skip counting patterns exhibited by equivalent fractions stand out. Note the equivalences of 1/2 and 2/3:
1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 6/12 = 8/16
2/3 = 4/6 = 6/9 = 8/12 = 10/15
Those for 1/2 are ripe for the question "What fraction is missing in this sequence?" Ans. 7/14, because the top numbers are counting numbers, so there should be a 7 between 6 and 8, and the bottom numbers are the skip counting numbers for 2, so there should be a 14 between 12 and 16.
|
 |